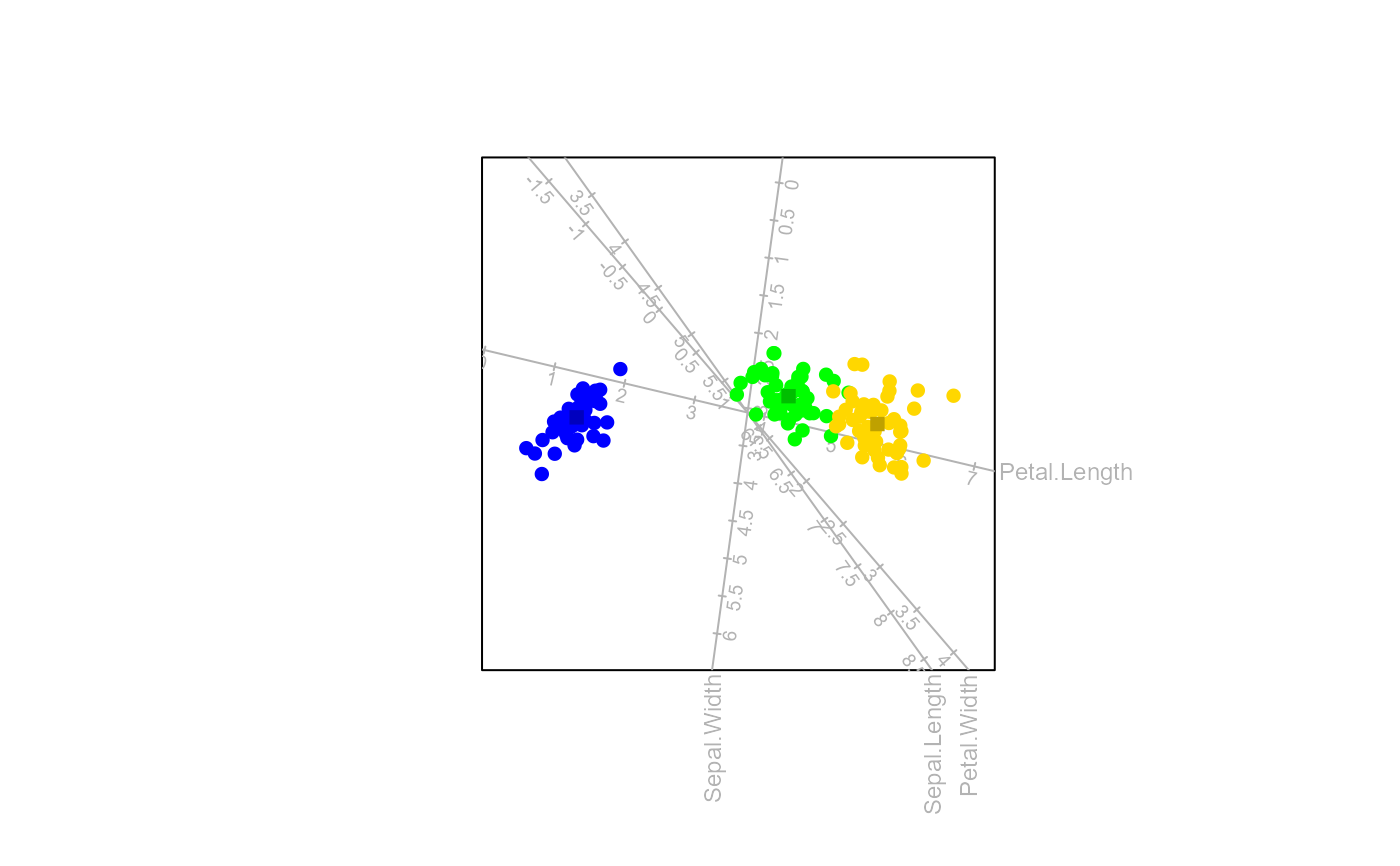
Perform Canonical Variate Analysis (CVA)

This function appends the biplot object with elements resulting from performing CVA.

Usage

CVA(bp, classes=bp$classes, dim.biplot = c(2, 1, 3), e.vects = 1:ncol(bp$X),
           weightedCVA = "weighted", show.class.means = TRUE,
           low.dim = "sample.opt")

Arguments

bp

an object of class biplot obtained from preceding function biplot().

classes

a vector of the same length as the number of rows in the data matrix with the class indicator for the samples.

dim.biplot

the dimension of the biplot. Only values 1, 2 and 3 are accepted, with default 2.

e.vects

the vector indicating which eigenvectors (canonical variates) should be plotted in the biplot, with default 1:dim.biplot.

weightedCVA

a character string indicating which type of CVA to perform. One of "weighted" (default) for a weighted CVA to be performed (The centring matrix will be a diagonal matrix with the class sizes (\(\mathbf{C} = \mathbf{N}\)), "unweightedCent" for unweighted CVA to be performed (The centring matrix is the usual centring matrix (\(\mathbf{C} = \mathbf{I}_{G} - G^{-1}\mathbf{1}_{G}\mathbf{1}_{G}'\))) or "unweightedI" for unweighted CVA to be performed while retaining the weighted centroid (The centring matrix is an indicator matrix (\(\mathbf{C} = \mathbf{I}_{G}\))).

show.class.means

a logical value indicating whether to plot the class means on the biplot.

low.dim

a character string indicating which method to use to construct additional dimension(s) if the dimension of the canonical space is smaller than dim.biplot. One of "sample.opt" (default) for maximising the sample predictivity of the individual samples in the biplot or "Bhattacharyya.dist" which is based on the decomposition of the Bhattacharyya distance into a component for the sample means and a component for the dissimilarity between the sample covariance matrices.

Value

Object of class CVA with the following elements:

X

the matrix of the centered and scaled numeric variables.

Xcat

the data frame of the categorical variables.

raw.X

the original data.

classes

the vector of category levels for the class variable. This is to be used for colour, pch and cex specifications.

na.action

the vector of observations that have been removed.

center

a logical value indicating whether \(\mathbf{X}\) is centered.

scaled

a logical value indicating whether \(\mathbf{X}\) is scaled.

means

the vector of means for each numerical variable.

sd

the vector of standard deviations for each numerical variable.

n

the number of observations.

p

the number of variables.

group.aes

the vector of category levels for the grouping variable. This is to be used for colour, pch and cex specifications.

g.names

the descriptive names to be used for group labels.

g

the number of groups.

Title

the title of the biplot rendered.

Lmat

the matrix for transformation to the canonical space.

Linv

the inverse of \(\mathbf{L}\).

eigenvalues

the vector of eigenvalues of the two-sided eigenvalue problem.

Z

the matrix with each row containing the details of the points to be plotted (i.e. coordinates).

ax.one.unit

one unit in the positive direction of each biplot axis.

Gmat

the indicator matrix defining membership of the classes.

Xmeans

the matrix of the class means.

Zmeans

the matrix of the class mean coordinates that are plotted in the biplot.

e.vects

the vector indicating which canonical variates are plotted in the biplot.

Cmat

the centring matrix based on different choices of weighting described in arguments.

Bmat

the between class sums of squares and cross products matrix.

Wmat

the within class sums of squares and cross products matrix.

Mrr

the matrix used for prediction from the canonical space (the inverse of \(\mathbf{M}=\mathbf{LV})\).

Mr

the first r dimensions of the solution to be plotted.

Nmat

the matrix with the class sizes on the diagonal.

lambda.mat

the matrix with the eigenvalues of \(\mathbf{W}^{-1/2}\mathbf{BW}^{-1/2}\) on the diagonal.

class.means

a logical value indicating whether the class means should be plotted in the biplot.

dim.biplot

the dimension of the biplot.

low.dim

the method used to construct additional dimension(s).

See also

biplot()

Examples

biplot(iris[,1:4]) |> CVA(classes=iris[,5])
#> Object of class biplot, based on 150 samples and 4 variables.
#> 4 numeric variables.
#> 3 classes: setosa versicolor virginica 
# create a CVA biplot
biplot(iris[,1:4]) |> CVA(classes=iris[,5]) |> plot()