Correspondence Analysis (CA) method

This function produces a list of elements to be used for CA biplot construction by approximation of the Pearson residuals.

CA(bp, dim.biplot = c(2,1,3), e.vects = 1:ncol(bp$X), variant = "Princ", 
lambda.scal = FALSE)

Arguments

bp

object of class biplot obtained from preceding function biplot(center = FALSE). In order to maintain the frequency table, the input should not be centered or scaled. For CA, bp should be a contingency table.

dim.biplot

dimension of the biplot. Only values 1, 2 and 3 are accepted, with default 2.

e.vects

which eigenvectors (canonical variates) to extract, with default 1:dim.biplot.

variant

which correspondence analysis variant, with default "Princ", presents a biplot with rows in principal coordinates and columns in standard coordinates. variant = "Stand", presents a biplot with rows in standard coordinates and columns in principal coordinates. variant = "symmetric", presents a symmetric biplot with row and column standard coordinates scaled equally by the singular values.

lambda.scal

logical value to request lambda-scaling, default is FALSE. Controls stretching or shrinking of column and row distances.

Value

A list with the following components is available:

Z

Combined data frame of the row and column coordinates.

r

Numer of levels in the row factor.

c

Numer of levels in the column factor.

Dr

Diagonal matrix of row profiles.

Dc

Diagonal matrix of column profiles.

Drh

Weighted row profiles.

Dch

Weighted column profiles.

rowcoor

Row coordinates based on the selected variant.

colcoor

Column coordinates based on the selected variant.

P

Correspondence Matrix.

Smat

Standardised Pearson residuals.

SVD

Singular value decomposition solution: d, u, v.

e.vects

Depending on what was specified in CA argument.

dim.biplot

The dimension of the biplot.

lambda.val

The computed lambda value if lambda-scaling is requested.

gamma

Contribution of the singular values, based on the CA variant.

See also

biplot()

Examples

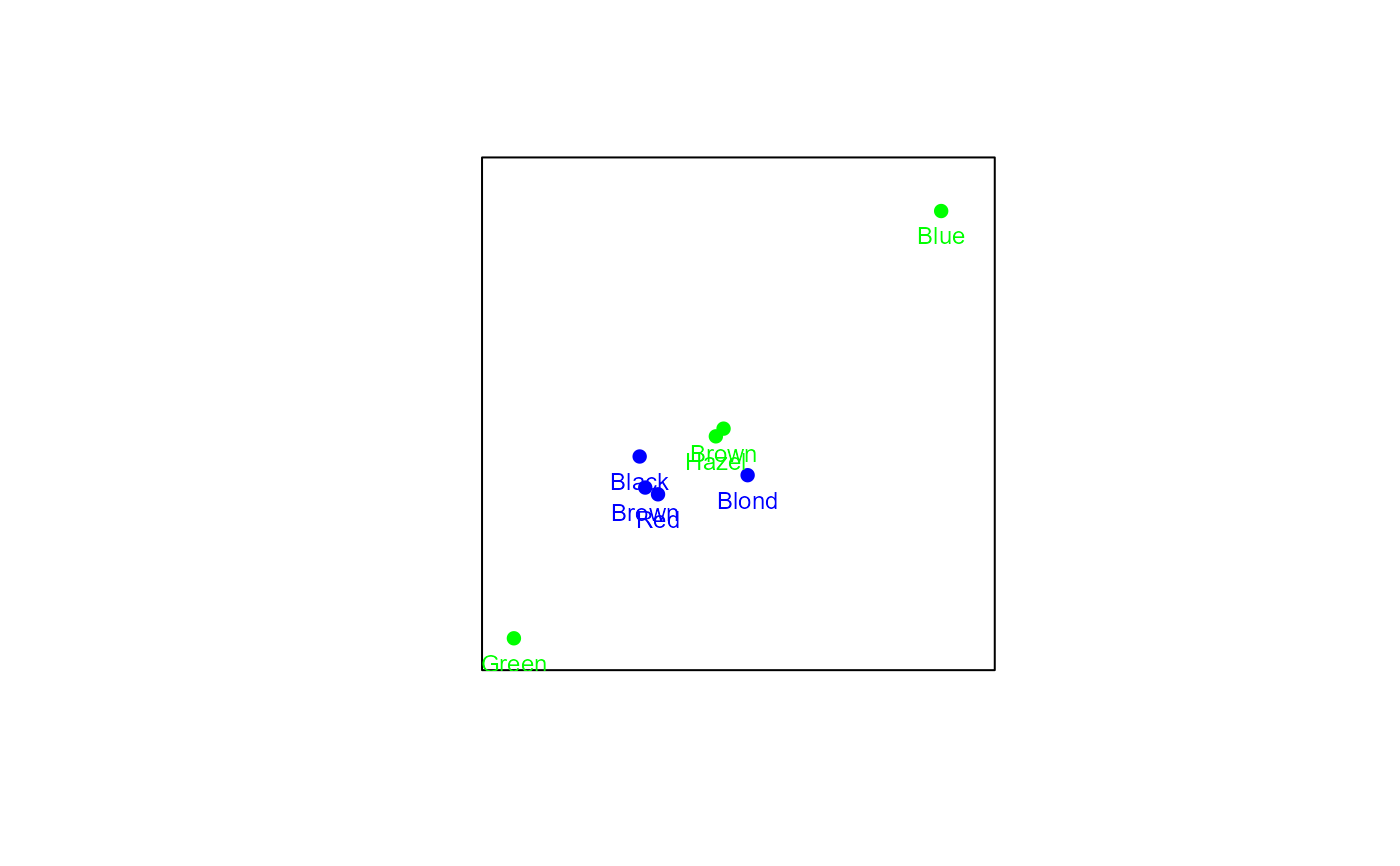
# Creating a CA biplot with rows in principal coordinates:
biplot(HairEyeColor[,,2], center = FALSE) |> CA() |> plot()

# Creating a CA biplot with rows in standard coordinates:
biplot(HairEyeColor[,,2], center = FALSE) |> CA(variant = "Stand") |> 
samples(col=c("magenta","purple"), pch = c(15,17), label.col = "black") |> plot()

# Creating a CA biplot with rows and columns scaled equally:
biplot(HairEyeColor[,,2], center = FALSE) |> CA(variant = "Symmetric") |> 
samples(col = c("magenta","purple"), pch = c(15,17), label.col = "black") |> plot()